The fretboard is something I was very afraid of when I planed to make my first ukulele. I thought it wouldn’t be accurate enough to measure the slot distances of an existing fretboard. So I wanted to understand how a fretboard works. Here comes some background for the interested ukulele makers.

If you double the frequency of a tone, you get one octave up. For example, the concert “a” has a frequency of 440 Hertz. The next higher “a” has a frequency of 880 Hertz. This explains why the 12^th fret is theoretically half the open string length (= 1/2 scale length). In the 12^th fret, you reach the same note, but one octave higher, and half the string length results in double the frequency.

Now we take for granted that there is a constant factor to get from one note to the next higher note. Otherwise the whole musical theory wouldn’t work. This leads to the following equations:
 

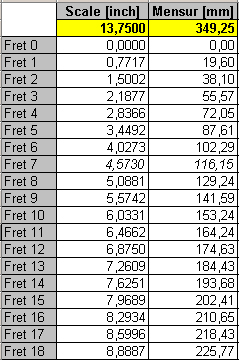
Example for standard soprano scale:

f0 = open string frequency, e. g. 440 Hz
f1 = 12^th fret frequency, e. g. 880 Hz
x = length factor from one fret to the next
lf_n = length of a fret
lf_n+1= length of the next higher fret
lf1 = length of 1st fret
ls = scale length

f0 / x¹² = f1 = 2 f0 => x = 2^1/12 = 1.059463 
=> lf_n / 1.059463 = lf_n+1

lf1 + lf1/x + lf1/x² + lf1/x³ + …+ lf1/x¹¹ = ls/2
=> lf1 = ls/17.81716

Example: scale length of 14”
Length of fret #1 = 14” / 17.81716 = 0.7858”
Length of fret #2 = 0.7858” / 1.059463 = 0.7417”
Length of fret #3 = 0.7417” / 1.059463 = 0.7000”
Length of fret #4 = 0.7000” / 1.059463 = 0.6607”
…

But unfortunately the theory doesn’t always match reality. Therefore you have to add 2 mm (1/12 inches) to the theoretical scale length. For our example this means that the distance from the nut to the bridge saddle is not 14”, but 14^1/12”. Why? The more you go up on the fretboard, the more you have to press the string down to bend it over the fretwire. This increases the string tension. Increasing the string tension is the same like tuning your string higher with the friction peg. This means your notes are too high the more you go up the fretboard. You can compensate for it by increasing the string length, because a longer string results in a lower frequency. How much you have to compensate depends on many factors, like the action of your ukulele, which means how high the strings are above the fretboard, but also the density of the string material has some impact.

Who is really interested in all these details should work with the Taylor formula. It shows which impact string length (l), frequency (f), string diameter (d) and string material density (Ro) have on the string tension (F).

Taylor formula:
F = (2l/f)² PI d²/4 Ro , PI = 3.14